Modellrechnung für einen mehrstufigen Fertigungsprozess.

Das Problem findet sich, mehr oder weniger ausgeprägt, in fast jeder Fabrik. Der Durchsatz bleibt unter dem eigentlich Möglichen, die Fertigungsbestände sind höher als nötig und die Terminsicherheit bietet Spielraum zum Bessern. Intuitiv wissen wir häufig, was schief läuft. Die Komplexität der Abläufe und wechselnde Engpässe verstellen aber den Blick auf die Lösung. Die folgende Betrachtung schafft Klarheit und zeigt einen Weg zur Lösung.

Analyse – Simulationsmodell

Der Fertigungsablauf soll mit einem einfachen Modell aus vier hintereinander liegenden Arbeitsbereichen A bis D dargestellt werden (siehe Grafik).

Entscheidend ist es, die Schwankungen des Durchsatzes in jedem Arbeitsbereich nachzubilden. Am einfachsten geht das mit einem Würfel. Die gewürfelte Punktezahl definieren wir als den (stark schwankenden) Durchsatz. Es entstehen Zahlenwerte zwischen eins und sechs, wobei jede Punktezahl die gleiche Wahrscheinlichkeit des Eintretens hat. Der mittlere Wert für den Durchsatz ist (1 + 6)/2 = 3,5. Würfelt man beispielsweise 10 Mal hintereinander, ergibt das in der Summe im Durchschnitt 35 Punkte.

Was bedeutet das für jeden der Arbeitsbereiche in der Kette? Jede Station kann maximal so viele Materialien verarbeiten und weitergeben, wie an Punkten gewürfelt wurden. Mit Ausnahme des ersten Arbeitsbereichs erhalten alle nachfolgenden Arbeitsstationen ihr Material von ihrem Vorgänger. Sie sind damit von dessen Durchsatz abhängig. Wenn in einem Arbeitsbereich eine höhere Kapazität (gewürfelte Punktezahl) zur Verfügung steht, kann dennoch nur das begrenzte, vom Vorgänger verfügbare, Material verarbeitet werden. Das bedeutet eine Verschwendung von Ressourcen.

Im umgekehrten Fall erreicht der Vorgänger einen hohen Durchsatz, während der Nachfolger nur eine kleinere Punktezahl erreicht. Das zur Verfügung stehende Material kann nicht in vollem Umfang verarbeiten werden. Die aktuelle Kapazität reicht dafür nicht aus. Bestand baut sich auf. Mit jedem Durchgang ändert sich die gewürfelte Zahl. So entsteht eine hohe Dynamik, die Auswirkungen auf alle anderen Arbeitsbereiche hat. In der Realität ist es ähnlich, nur die Gründe sind andere: Mitarbeiter können nicht tätig werden, weil Vorrichtungen nicht zur Verfügung steht, es fehlt Material, Qualitätsprobleme im Prozesse, etc.

Dieses Simulations-Modell kann man mit einfachen Mitteln auf einem Tisch nachspielen. Es wurde 1984 von Eliyahu Goldratt in seinem Buch „The Goal“ beschrieben. Zur Veranschaulichung haben wir in Excel eine Simulation programmiert, die genau den gleichen Spielregeln folgt. Siehe dazu: www.schmid-wolff.de/simulation_lieferketten.html

Dynamische Engpässe

Mit dieser Excel Modell-Simulation lässt sich nun veranschaulichen, wie sich eine Fertigungslinie unter dem Einfluss von Prozess-Schwankungen verhält. Die wechselnden Bestandshöhen in den einzelnen Arbeitsbereichen zeigen, dass sich im Ablauf immer wieder neue Engpässe ergeben, vor denen sich das Material „staut“. Im Gegensatz zu statischen Engpässen spricht man hier von dynamischen Engpässen. Sie sind ein charakteristisches Erscheinungsbild in vielen Produktionen. Weil sie so dynamisch sind, lassen sie sich nur schwer messen und beherrschen. Weiter lässt sich beobachten, dass der Durchsatz mit dem Fertigungsfortschritt abnimmt. Ursache sind die beschriebenen gegenseitigen Abhängigkeiten der Arbeitsbereiche und die Schwankungen des Durchsatzes. Man erkennt, dass der Output am Ende des Prozesses nicht konstant ist, sondern erheblichen Schwankungen unterworfen ist. In der Praxis gibt man, um knappe Termine zu halten, bestimmten Aufträgen häufig eine höhere Priorität. Bei gleichen Randbedingungen verschlimmert das jedoch die Situation. Der mit Priorität versehene Auftrag läuft schneller durch – zu Lasten von anderen Aufträgen. Die dadurch verzögerten Aufträge bekommen zu einem späteren Zeitpunkt ebenfalls Priorität. Das Spiel beginnt von vorne. So erzeugt das „System“ aus sich selbst heraus ein erhebliches Maß an Unruhe und Stress für alle Beteiligten.

Die nachstehende Abbildung 1 zeigt das Resultat von starken Schwankungen im Durchsatz:

Die Durchlaufzeit (DLZ) durch den gesamten Fertigungsprozess unseres Modell-Beispiels streut sehr stark. Eine termingenaue Steuerung der Fertigung ist fast unmöglich.

Mit einem Simulationswerkzeug (unser Excel-Programm) kann man Parameter verändern und die Reaktion des Systems studieren. Nun limitieren wir die Schwankungen. Dazu nutzen wir einen künstlichen Würfel, der nicht mehr zwischen eins und sechs schwankt sondern nur noch zwischen zwei und fünf (Szenario 2) oder zwischen drei und vier (Szenario 3). Der Mittelwert von 3,5 bleibt gleich. Die negativen Effekte lassen deutlich nach und die Produktivität des Systems steigt stark an (vgl.: Abbildung 5).

Abbildung 2:

Kleinere Schwankungen im Durchsatz – höhere Produktivität und geringere Bestände.

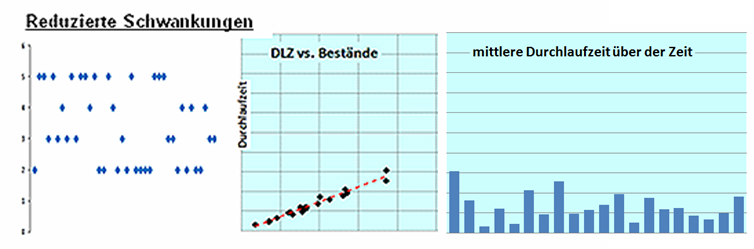
Abbildung 3:

Weiter reduzierte Schwankungen – noch höhere Produktivität im System (Szenario 3).

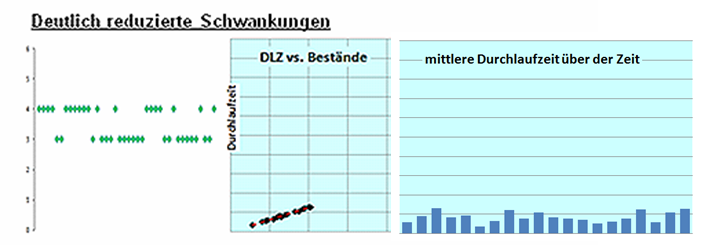
Vergleicht man die Häufigkeitsverteilungen der Durchlaufzeiten für den gesamten Fertigungsprozess, wird der Effekt durch reduzierte Schwankungen noch augenfälliger: Der Ablauf wird sehr viel schneller!

Abbildung 4 stellt die Schwankungen der Durchlaufzeit (DLZ) in den drei Szenarien dem Output (Abb. 5) gegenüber:

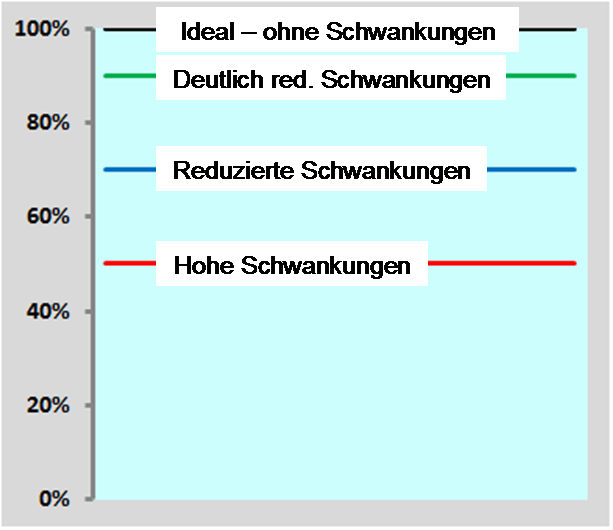
Eine unmittelbare Folge reduzierter Schwankungen ist ein Anstieg des Output bzw. der Produktivität von etwa 50% (Szenario 1) auf über 90% (Szenario 3).

Abbildung 5:

Geringe Prozessschwankungen – hohe Produktivität.

Maßnahmen –> Stabile Prozesse

Als erstes wird man versuchen, Schwankungen so weit wie möglich zu reduzieren. Dazu bedarf es der gründlichen Ursachenanalyse innerhalb jeder Arbeitsstationen. Reale Fertigungsprozesse werden nie ganz ohne Schwankungen arbeiten. Mit einem gewissen Maß an Schwankungen muss man also leben.

Im zweiten Schritt geht es darum, zu verhindern, dass sich diese restlichen Schwankungen vom Vorgänger zum Nachfolger fortpflanzen. Solche Entkopplungsmechanismen sind situationsangepasst unterschiedlich. Eine Methode ist, angemessene zeitliche Puffer vorzusehen: Für jeden Auftrag und Prozessschritt gibt es einen vorgegebenen Start- und Endzeitpunkt. Darin ist ein gewisser Zeitpuffer enthalten. Die Mitarbeiter sind nun in der Lage dafür zu sorgen, dass der vorgegebene Endzeitpunkt immer eingehalten wird. Der nächste Fertigungsabschnitt kann sich darauf verlassen, dass zu seinem Auftragsbeginn alle Voraussetzungen für einen optimalen Ablauf gegeben sind.

Abbildung 6: Beispiel für Auftragsdurchlauf über zeitdefinierte und entkoppelte Arbeitsprozesse.

Die Effizienz (Wirkungsgrad) des Gesamtprozesses ist sehr hoch, liegt jedoch unter dem theoretischen Maximal-Wert. Die eingebauten Puffer kosten etwas Produktivität. Der gesamte Ablauf ist jedoch wesentlich stabiler und robuster (siehe Grafik).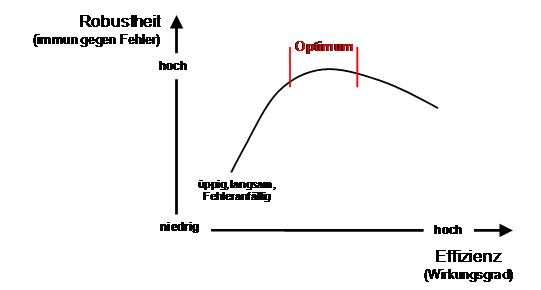
Die Notwendigkeit von spontanen Veränderungen der Prioritäten entfällt. Die Belastung aller Beteiligten sinkt deutlich.

Literatur:
Goldratt, Eliyahu: The Goal. Excellence in Manufacturing; 1984
(auf Deutsch: Das Ziel; 2002 Campus Verlag, Frankfurt)

© 2009 Schmid & Wolff